vol I chap 1 sect 2
Previous: 1.1. Mathematics and science in ancient Greece.
1.2. Conceptualizations of spaces and quantum statistics.¶
The first part of this section is based on the conference Géométrie et astronomie sphérique dans la première cosmologie grecque by Jean-Pierre Vernant (1963). All the considered conceptualizations of space as democratic or dictatorial were accomplished before the Christian era. The second part refers to a building process in quantum statistics where particles are classified in families according to criteria that can be referred as democratic or dictatorial.
Circular spaces in political organizations and astronomical and geometrical spaces.¶
Before political institutions were established in Greece, the highest level in the social organization was occupied by the king-priest. The entire population was always under conditions of domination and submission. There were no spaces for communications. Public affairs were not discussed, they were imposed. However, laws and rules were promulgated and made public in written.
Vernant considered how the evolution of ancient Greek society generated two kinds of conceptual developments in social contexts related to the conceptuaization of space:
(1) the building of circular spaces in family life and community (the reference is made to the philosopher Pherecydes, the historian and geographer Herodotus, the poet Homer, and the architect Hippodamus), and
(2) the concept of circularity in the definition of astronomical spaces (reference is made to the poet and philosopher Hesiod and to the philosopher, geographer and physicist Anaximander).
When Greek cities were built (the polis) writing was used as a transforming instrument that made public private issues. Probably it was Pherecydes of Syros (580 BC – 520 BC) the first writer to publish a philosophical work in prose. He wrote books for transforming private knowledges into public possibilities for discussion. Herodotus of Halicarnassus (484 BC- 425 BC) mentioned that when the dictator Polycrates of Samos died, his successor asked all the citizens to meet in an assembly and informed them that he will behave in a democratic way in total disagreement with his predecessor

|

|
|---|
Homer (VIII century) wrote in Odyssey (chant II) that Telemachus, son of Ulysses and Penelope, was worried because many pretenders to the throne were harassing his mother. He asked soldiers to protect her by forming an agora (Greek word for an assembly). It is attributed to the same writer the use of the word ageirien laon, that means to congregate the army.
One of the first urban architects Hippodamus of Miletus (498 BC- 408 BC) rebuild Miletus around 479 BC. The city was sacked and destroyed by Persians in 490 BC. The map made by Hippodamus shows an ordered reticular structure having an agora as its center with broader and straight streets.

|

|
|---|
According to Vernant, the new image of the democratic Greek society went in parallel with a new image of the astronomical and geometrical spaces. This conceptual change implied overcoming astronomical Babylonian ideas as well as eliminating myths about the form of the Earth.
Astronomy in Babylon characterized a religion believing that stars were divinities whose intentions might be perceived if their positions in the sky were carefully observed and registered. Scribes serving the king were in charge for registering the economic activity of the kingdom and for accounting all celestial and terrestrial events. Their knowledge was arithmetic without connections to any geometrical system of spatial representations of positions and movements. However, Greek ancient astronomy was looking for explanations about the structure of the world without appeal to divinities nor ritual ceremonies, although it was full of myths.
Hesiod of Askra; Thebes (nearby 800 BC) wrote a Theogony, a mythological treatise describing the origin of gods. According to him the Earth was a vessel whose interior contained a structured world enclosed by Zeus to avoid the perception of light in the disordered world: at the upper level lived Zeus and immortal gods, then the human beings and downward death and underground gods.
Anaximander of Miletus, Ionia, (619 – 546) had a spherical notion of the universe whose center contained the Earth as a cylindrical column at equilibrium, stagnant and without falling. This was a democratic conceptualization of space were all positions and distances were mathematically defined.

|

|
|---|
The agora.
As a part of a demystification and rationalization process of the social life, the agora was a center for political actions and decisions with social, urban and cultural implications for the community. In that place democracy and law application were expressions of equality, equilibrium, symmetry and reciprocity. This was an indication of the appearance of new politically centralized institutions.
Just for comparison, it is interesting to observe the presence of meeting regions in the following archeological sites:
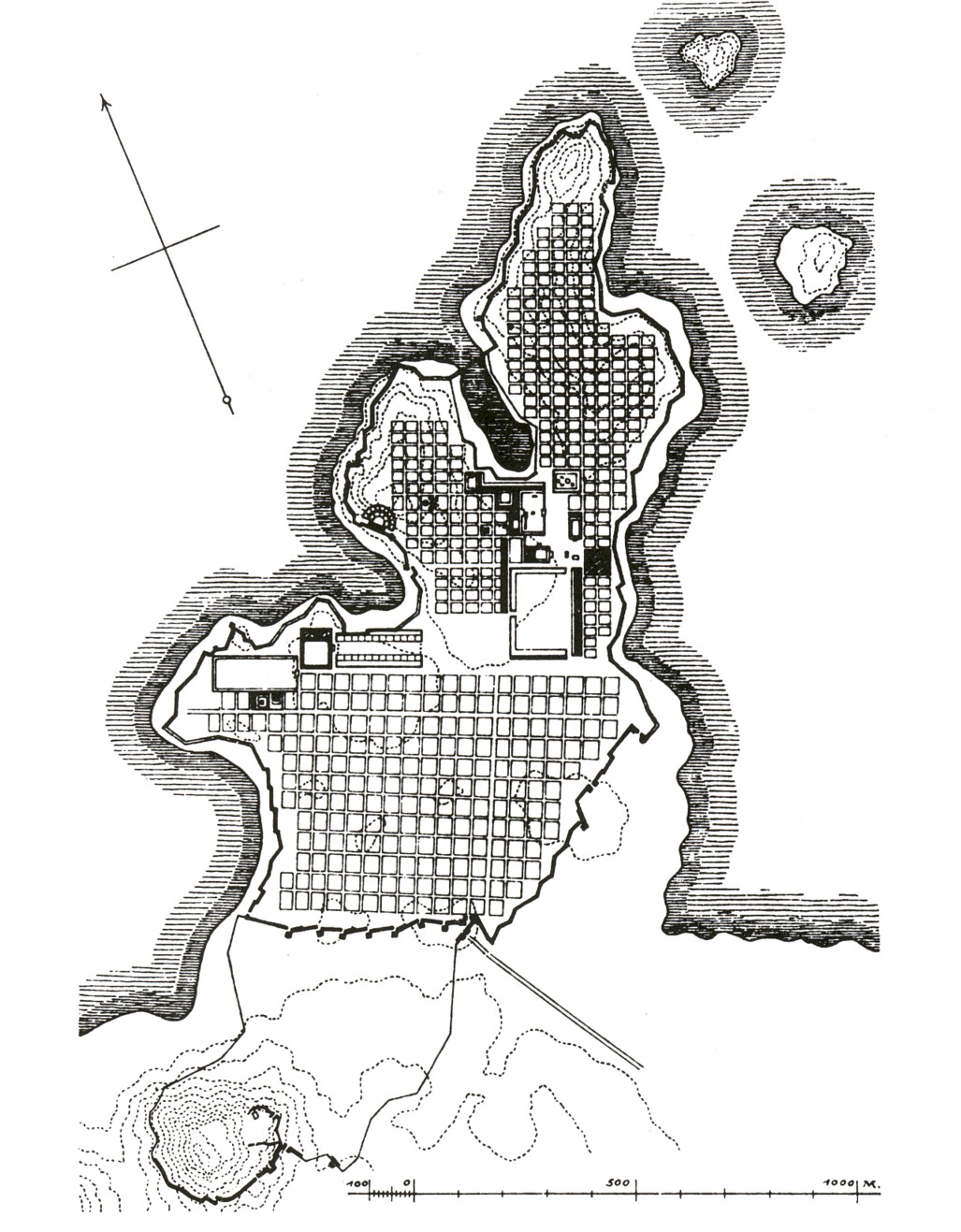
Plan of Milet in the Classical period, nearby 490 BC.

Sun pyramid in Teotihuacan, Mexico, nearby 450 AC.
Residential palace in Machu Pichu, Peru, nearby 1500 AC.
Massada in Israel, nearby 20 BC
For a broader treatment concerning conceptualization of spaces, see the following references:
https://en.wikipedia.org/wiki/Cognition and https://en.wikipedia.org/wiki/Spatial_cognition
Cognitive spaces in quantum statistics: fermions or bosons.¶
In what follows, the conceptualization of spaces as dictatorial or democratic will be applied to the classification scheme of elementary particles concerning quantum statistics that separates fermions (contributions made by Pauli) from bosons (contributions made by Born). In a sense, fermions show a dictatorial behavior and bosons a democratic one.
The notion of quantum statistics is now analyzed by looking at two Physics Nobel Prizes: the 1945 Prize to Wolfgang Pauli “for the discovery of the Exclusion Principle, also called the Pauli Principle”, and the 1954 Prize to Max Born “for his fundamental research in quantum mechanics, especially for his statistical interpretation of the wavefunction”. The 1945 Prize was also awarded to Walther Bothe "for the coincidence method and his discoveries made therewith".In what follows, for each Nobel Laureate we include a brief description of his work as presented in the document called WORKS published in the Nobel wave page and indicate the titles of their Nobel Lectures. References for both documents are mentioned in MLA format (MLA means Modern Language Association).
Furthermore, each Nobel Lecture is described in a two columns Table: one column is for Accepted knowledge or questions under discussion in Laureate´s time and another column is for Laureat´s contributions or explanations. Quotation marks indicate complete quoted paragraphs.
1945 Physics Nobel Prize awarded to Pauli.¶
WORK: "In Niels Bohr’s model of the atom, electrons move in fixed orbits around a nucleus. As this model developed, electrons were assigned certain quantum numbers corresponding to distinct states of energy and movement. In 1925, Wolfgang Pauli introduced two new numbers and formulated the Pauli principle, which proposed that no two electrons in an atom could have identical sets of quantum numbers. It was later discovered that protons and neutrons in nuclei could also be assigned quantum numbers and that Pauli’s principle applied here too."
MLA style: Wolfgang Pauli – Facts. NobelPrize.org. Nobel Prize Outreach AB 2023. Sat. 25 Feb 2023. https://www.nobelprize.org/prizes/physics/1945/pauli/facts/
NOBEL LECTURE: Exclusion Principle and Quantum Mechanic by Pauli.
MLA style: Wolfgang Pauli – Nobel Lecture. NobelPrize.org. Nobel Prize Outreach AB 2023. Sat. 25 Feb 2023. https://www.nobelprize.org/prizes/physics/1945/pauli/lecture/

1954 Physics Nobel Prize awarded to Born.¶
WORK: "In Niels Bohr’s theory of the atom, electrons absorb and emit radiation of fixed wavelengths when jumping between orbits around a nucleus. The theory provided a good description of the spectrum created by the hydrogen atom, but needed to be developed to suit more complicated atoms and molecules. Following Werner Heisenberg’s initial work around 1925, Max Born contributed to the further development of quantum mechanics. He also proved that Schrödinger’s wave equation could be interpreted as giving statistical (rather than exact) predictions of variables."
MLA style: Max Born – Facts. NobelPrize.org. Nobel Prize Outreach AB 2023. Sat. 25 Feb 2023. https://www.nobelprize.org/prizes/physics/1954/born/facts/
NOBEL LECTURE: The Statistical Interpretations of Quantum Mechanics by Born.
MLA style: Max Born – Nobel Lecture. NobelPrize.org. Nobel Prize Outreach AB 2023. Sat. 25 Feb 2023. https://www.nobelprize.org/prizes/physics/1954/born/lecture/

Next: 1.3. Contexts learning for conceptualizing cognitive spaces.